This document describes the relation ship between the voltage on PIN 7 and the deviation in part per billion (ppb)

On the diagram below you can see the applied voltage on the X-axis and the offset in ppb on the Y-axis

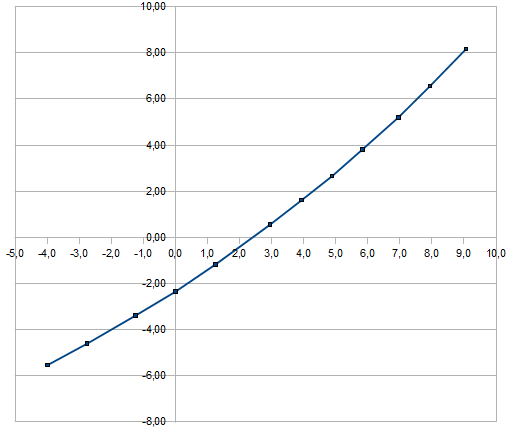
efratom_voltage_adjust.png

The following formula calculates the offset as function of the voltage:

f(x) = -2.2426 + 0.927099 * x + 0.026193 * x^2

Using the UNIX “dc” command to calculate for example for x=0 :

export X=0 ; dc <<< "20k _2.2426 0.927099 $X * + 0.026193 $X d ** + p"
-2.242600

The inverse function describes the voltage as function of the offset:

f(y) = 2.242 + 0.989116 * y - 0.0216413 * y^2

export Y=0 ; dc <<< "20k 2.242 0.989116 $Y * + _0.0216413 $Y d ** + p"
2.2420000

Hint: for negative numbers one has to use the underscore. It’s “dc” behavior.

export Y=_4 ; dc <<< "20k 2.242 0.989116 $Y * + _0.0216413 $Y d ** + p"
-2.0607248

I made 2 measurements

This one is made with the trimmer in position counter clockwise

voltage   ppb
-3,985   -5,53
-2,750   -4,60
-1,250   -3,39
0,000   -2,35
1,255   -1,17
2,945   0,55
3,940   1,62
4,890   2,66
5,830   3,81
6,960   5,21
7,940   6,56
9,060   8,16

Here the timer is turned clockwise

voltage   ppb
-3,960   -5,52
-2,984   -4,76
-1,253   -3,36
0,000   -2,23
1,253   -1,04
3,125   0,90
3,920   1,77
5,020   3,08
5,960   4,21
7,140   5,74
8,050   6,91
8,930   8,12

Actually there are no differences except some measuring inaccuracy.

Of course this is only true for my EFRATOM. Yours has maybe a different trajectory.